보정이란 일반 방사성탄소 연대 [Conventional Radiocarbon Age – (δ13C 값을 이용해 동위원소 분별로 교정한 BP 연대)]를 우리가 사용하는 달력 상의 연대로 전환할 때 적용합니다.
보정에 사용하는 기준은 약 13,900 BP까지의 결과 값을 이미 알고 있는 참나무, 세쿼이야, 전나무의 나이테 시료 수백개의 정확한 방사성탄소 연대을 통해 구합니다. 그 이상 연대의 경우, 약 55,000 BP까지는 다양한 여러 종류의 증거를 사용해 만듭니다. 이런 정보들은 국제적으로 승인된 데이터 베이스로 만들어지며, 계속 업데이트 되어 가고 있습니다. 현재 사용하는 데이터베이스는 북반구의 경우 IntCal20 , 남반구의 SHCal20 와 해양 상태에서의 Marine20 입니다.
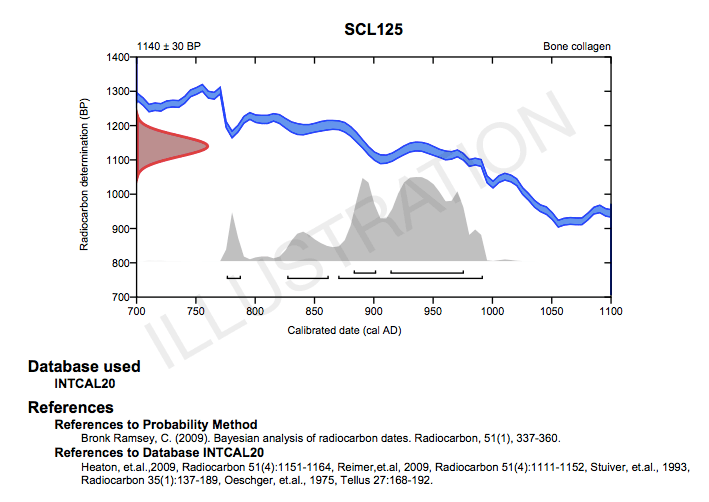
최근 많은 연구자들은 일반 방사성탄소 연대를 보정할 때 수학적 방법을 사용하면서 통계학적 방법으로 정제된 방법을 많이 사용합니다. 이 통계적 정제 방법이란 95.4 와 68.2 확률 내에서 하나의 보정 범위를 다른 범위의 “가능성” (likelihood)을 확인하는 것입니다. 이런 가능성이란 플롯 있는 회색 부분으로 그래프 상에서는 보여주며, 백분율 값을 다음 범위에 보여줍니다. 이 방법을 고확률 밀도 범위 법이라 부릅니다.
해양 탄산염 시료의 보정은 전지구적 리저브어 영향과 지역 리저브어 영향(global and local geographic reservoir effects) 모두 고려해야 합니다. 민물 탄산염 (“경수 효과 (hard water effect)라는 용어로 쓰임) 의 리저브어 효과는 알려져 있지 않으며, 적용하기기 쉽지 않습니다.
면책조항: 이 비디오는 제3자의 사이트에 올렸으며, 광고가 포함되어 있습니다.
이 비디오 인용은 Beta 연구소 웨비나의 일부입니다. 동위원소 기초: 동위원소 분석 소개
목재나 목탄 시료의 경우, “고목 영향 (old wood effect) 과 더불어 젊은 물질의 침투를 항상 고려해야 합니다. 탄산염 시료의 경우, 리저브어 보정은 이론적이지만 지역 변동은 실제 일어나며, 상당히 변화가 심하며, 시료가 어디서 왔는지에 영향을 많이 받습니다. 프로그램에 의해 생성된 연대 범위는 반드시 대략적이라는 것을 염두에 두어야 합니다. 방사성탄소 연대에 인용된 오차범위는 (+/- X BP) 보정 단계에서 사용되며, 오차 범위 결정에 매우 엄격히 제한되어 있습니다. (시료, 현대의 C14 표준 및 백그라운드 시료의 카운팅 오차), 시료의 균질성 문제, 성장 나이테의 위치 (고목 영향의 가능성) 시료의 재배치 (재퇴적), 수중 시료의 지역 리저브어 영향들과 같은 불명확한 오차들은 항상 수량화 할 수 없으며, 해석할 때 항상 이들을 고려해야 합니다.
2021년 1월 업데이트